Velkommen til Regn Lyden Ud - i matematiktimen - et online undervisningsmateriale, der sætter fokus på matematikken bag kunstig intelligens.

Regn Lyden Ud er et klassesæt for 3. G. til brug i matematik A.

Materialet viser jer, hvordan kunstig intelligens bare er matematik og logik, og hvordan I kan bruge matematik til at lave og træne jeres egen kunstige intelligens.

Vi slutter af med en øvelse, hvor I selv skal optage og arbejde med lyde.

Og nej: I er ikke helt klar til at kode den næste udgave af SIRI eller Skynet fra Terminator, når I er færdige med det her forløb. Men I får styr på, hvordan kunstig intelligens fungerer, og I kan bygge og træne såkaldte neurale netværk, som kan genkende lyde.

Rigtig god fornøjelse!

Klassifikation - et centralt element i læring

Noget af det vigtigste i al læring - både for mennesker og computere - er at kunne klassificere input. Hvis man f.eks. vil lære at cykle, er det vigtigt at vide, hvornår man er kørt succesfuldt fra A til B, og hvornår man i stedet er faldet ud over styret og landet i en hæk. Jo mere sikker man er på, om det ene eller det andet er indtruffet, jo nemmere er det at lære af sine erfaringer.

Derfor introducerer vi i dette afsnit begrebet klassifikation - fortolkning og inddeling af data i kategorier. Det er et område, vi beskæftiger os med i resten af denne opgavesamling, og som er helt centralt i kunstig intelligens.

Regression

Men vi starter på mere velkendt territorium: Du har sikkert stiftet bekendtskab med begrebet regression, hvor vi forsøger at finde en funktion, som bedst muligt beskriver nogle givne datapunkter.

Mere generelt kan vi sige, at givet $N$ datapunkter $(x_{1}, y_{1}), . . ., (x_{N}, y_{N})$ ønsker vi at finde en funktion $\hat{y} = f (x)$ således at summen af kvadratet på fejlene, vi begår, ved ovenstående approksimation bliver mindst muligt.

Beregningen af fejlen (summen af de kvadrede afvigelser) ser således ud:

$\sum_{i = 1}^{N} ({\hat{y}}_{i} - y_{i})^{2}$

Nært beslægtet med regression er begrebet klassifikation.

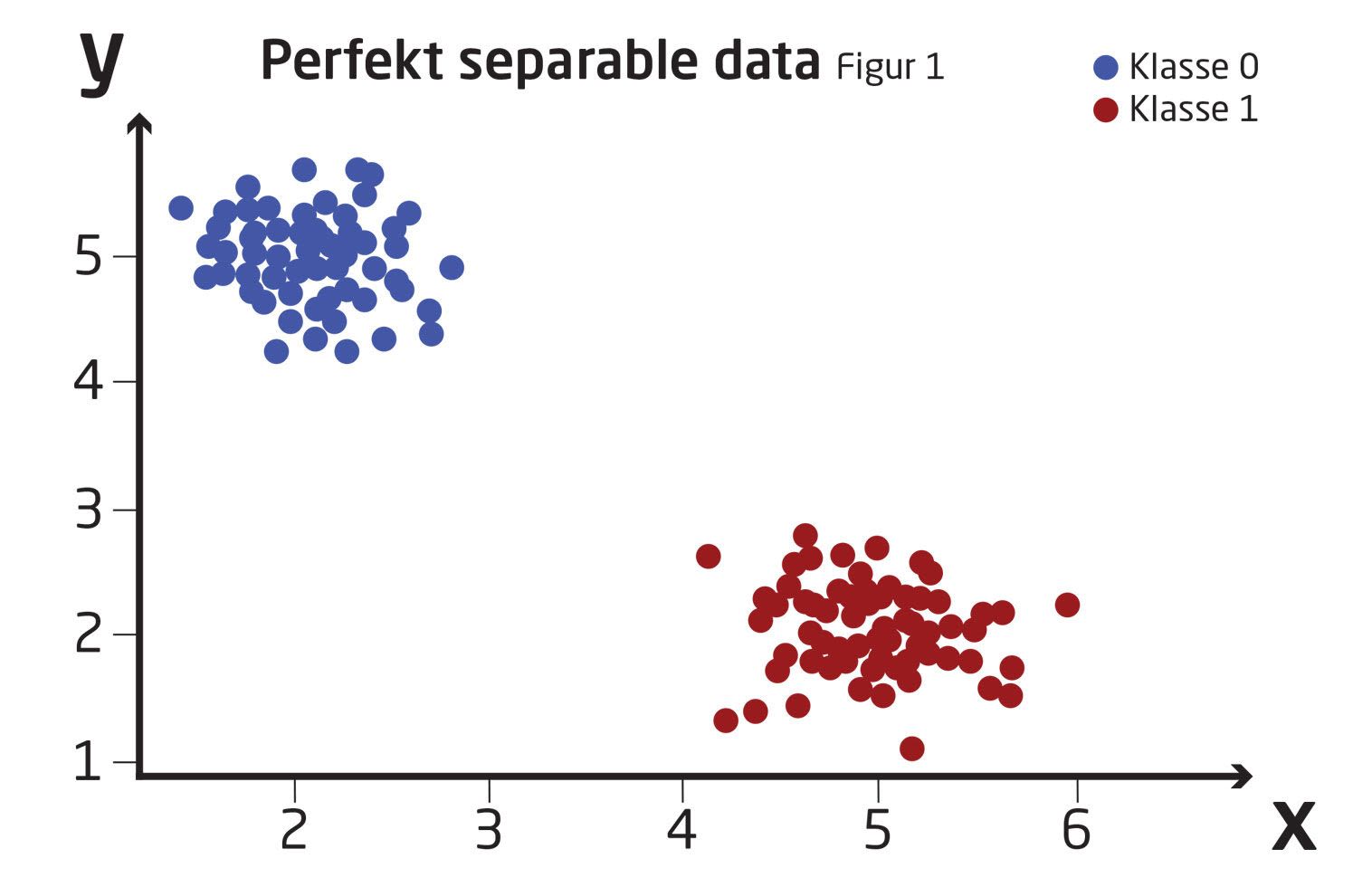
Forestil dig, at vi er givet følgende data, der fordeler sig i et koordinatsystem som vist i figur 1.

De blå punkter er medlemmer af én klasse, og de røde punkter er medlemmer af en anden. Vi kunne f.eks. kalde klasserne 0 og 1.

Hvor vi med regression ønsker at finde en funktion, der ligger tæt på vores punkter, kan vi tænke på klassifikation som at finde en funktion, der bedst adskiller vores punkter.

I dette tilfælde her er det ret simpelt at løse problemet i hånden ved simpelthen at tegne en linie som adskiller de to klasser af punkter.

Opgave 1

A) Kan du finde forskriften for en lineær sammenhæng $y = a x + b,$ der perfekt separerer de to klasser?

B) Der findes mange sammenhænge, der separerer klasserne perfekt. Er nogle løsninger bedre end andre? Hvorfor? Prøv at sammenligne dit svar med sidemandens, eller med resten af klassen.

Hvis man kan løse et klassifikationsproblem, således at ingen datapunkter ender i den forkerte klasse, kalder vi datasættet for perfekt separabelt. Dette svarer på en måde til et regressionsproblem, hvor alle datapunkter falder perfekt på en linie - bare modsat: Ingen punkter falder på linien. Sådanne problemer forekommer sjældent i den virkelige verden og er derfor ikke særlig interessante.

I opgaven ovenfor var det nemt at finde en lineær sammenhæng, der separerede (klassificerede) vores data. Men vores fremgangsmåde er af flere grunde ikke særlig anvendelig for en kunstig intelligens, dette skyldes bl.a:

At data i virkeligheden yderst sjældent sorterer sig så pænt som i opgaven.
At vores løsning til opgaven kræver, at vi kan se, om et datapunkt ligger under eller over en linie, og det kan vores computer ikke.

I virkeligheden ser vores data oftere ud som på figur 2.

Igen vil vi gerne finde en funktion, der deler vores data op i to klasser. Nu er problemet dog noget mere kompliceret, da vi ikke bare kan tegne en linje, der perfekt separerer de to klasser. Vi må derfor finde en bedre og mere sofistikeret måde at adskille vores data.

Vi vil opstille en matematisk model, der løser vores klassifikationsproblem. En matematisk model er en funktion, der som input tager vores datasæt og som output giver et tal, der fortæller os, hvilken klasse vores datapunkter tilhører.

I eksemplet fra Figur 1 kunne vores model f.eks. være givet som $f (x, y) = y - x$ , såldes at når $f (x, y) > 0$ , så klassificerer vi et datapunkt, $(x, y)$ , som tilhørende klasse 0. Og tilsvarende klassificerer vi $(x, y)$ som tilhørende klasse 1, hvis $f (x, y) < 0$ .

Opgave 2

A) Modellen $f (x, y) = y - x$ svarer til, at vi bruger den lineære sammenhæng $y = x$ til at adskille vores datapunkter.

B) Forklar hvorfor dette er sandt og hvorfor $f (x, y) = y - x$ fungerer bedre i et neuralt netværk.

Hjælp: Overvej hvilke typer af input vores model har brug for.

Vi ved nu hvad et klassifikationsproblem er, og hvordan man kan adskille perfekt separable data. I virkeligheden bruger man dog sjældent... faktisk stort aldrig... kunstig intelligens til at adskille perfekt separable data. Spørgsmålet er derfor, om vi kan opstille modeller, der er i stand til at klassificere overlappende, langt mere rodede datasæt. For at gøre det skal vi bl.a. se på begrebet konfidens, og vi skal introducere en ulinearitet i vore neuroner ved hjælp af aktiveringsfunktioner (som kan opfattes som en bedre og mere computeregnet måde at lave ikke lineære funktioner... mere om det i næste afsnit.)

Aktiveringsfunktioner og konfidens

I dette afsnit skal vi se, hvordan vi matematisk finder gode klassifikationsmodeller, når vi har med ikke-separable data at gøre. Vi skal derudover introducere neurale netværk. Så lad os starte med at introducere de byggeklodser, de neurale netværk er opbygget af. Den første byggeklods er neuronerne.

Idéen bag et neuralt netværk er, at en samling af simple matematiske funktioner samarbejder om at skabe en avanceret funktion - lidt som i biologien og i den menneskelige hjerne. Derfor kaldes hver enkelt af de simple matematiske funktioner også neuroner. Nedenfor kan du se et eksempel på en simpel matematisk funktion - eller neuron - som den bruges i et neuralt netværk.

Det lineære neuron

Vi skal prøve at opbygge en klassifikationsmodel ved hjælp af neuroner.

Det simpleste neuron, vi kan arbejde med, er lineært, og modtager blot et enkelt input. Neuronet er afbildet på to måder her:

I figurene ser vi således ét neuron (grønt), som modtager et en-dimensionelt input, $x$ (rødt). Neuronet fungerer ved at gange input $x$ med en vægt, $w_{x}$ , og lægge et bias $b$ til. Dette simple neuron kan beskrives som en lineær funktion, som tager $x$ som input, og giver output $\hat{y}$ (blåt), således at,
$\hat{y} = f (x) = w_{x} \cdot x + b$

Dette neuron opfører sig altså blot som en lineær funktion $f (x) = a \cdot x + b$ . Her har vi bare omdøbt $a$ i til $w_{x}$ . Dette skyldes at $w_{x}$ normalt kaldes vægte (weights) når man beskæftiger sig med neurale netværk. Vi vil fremadrettet referer til $w_{x}$ og $b$ som modelparametre.

Aktiveringsfunktioner

Vi har nu introduceret det lineære neuron. Dette er en af vores byggesten, når vi skal bygge neurale netværk. Det er dog ikke alle problemer, vi kan løse med linære funktioner. Vi har derfor brug for at introducere en ikke-linearitet i vores netværk. Dette vil vi gøre via såkaldte aktiveringsfunktioner.

Ideen er simpel: Vi vil tage en ikke-lineær funktion på outputtet fra vores lineære neuron. Vores lineære funktion med efterfølgende aktiveringsfunktion kan ses her:

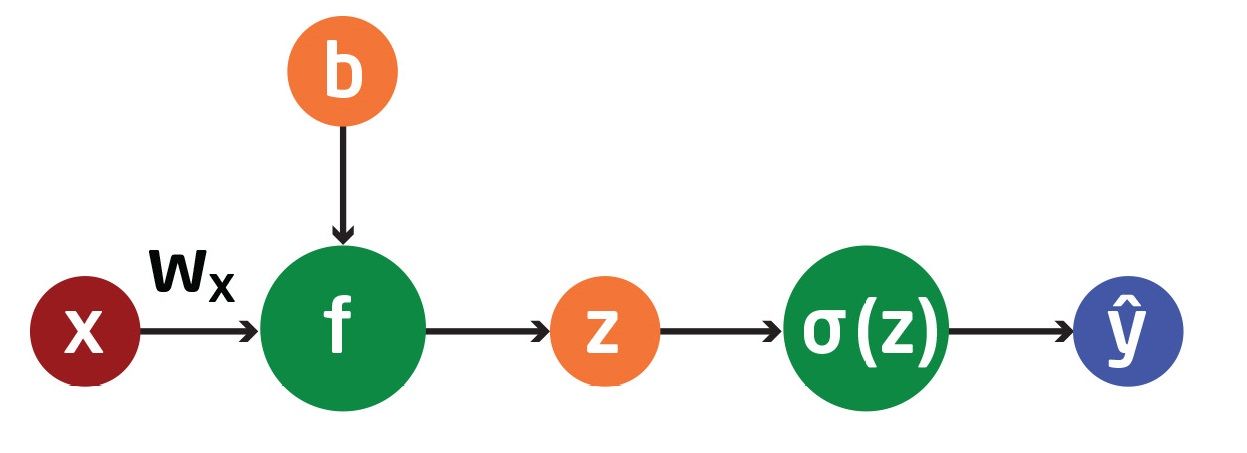
Her har vi omdøbt outputtet fra vores lineære neuron fra $\hat{y}$ til $z$ , da det ikke længere er dette output, der er vores forudsigelse, men blot outputtet fra vores lineære neuron.

Der er ingen begrænsning på, hvilke funktioner vi kan vælge som aktiveringsfunktioner. Der er dog tre vigtige aktiveringsfunktioner, vi ofte bruger, da de har vist sig at virke godt. Disse funktioner er:

Sigmoidfunktionen som er givet ved:

$σ (z) = 1 / (1 + e^{- z})$

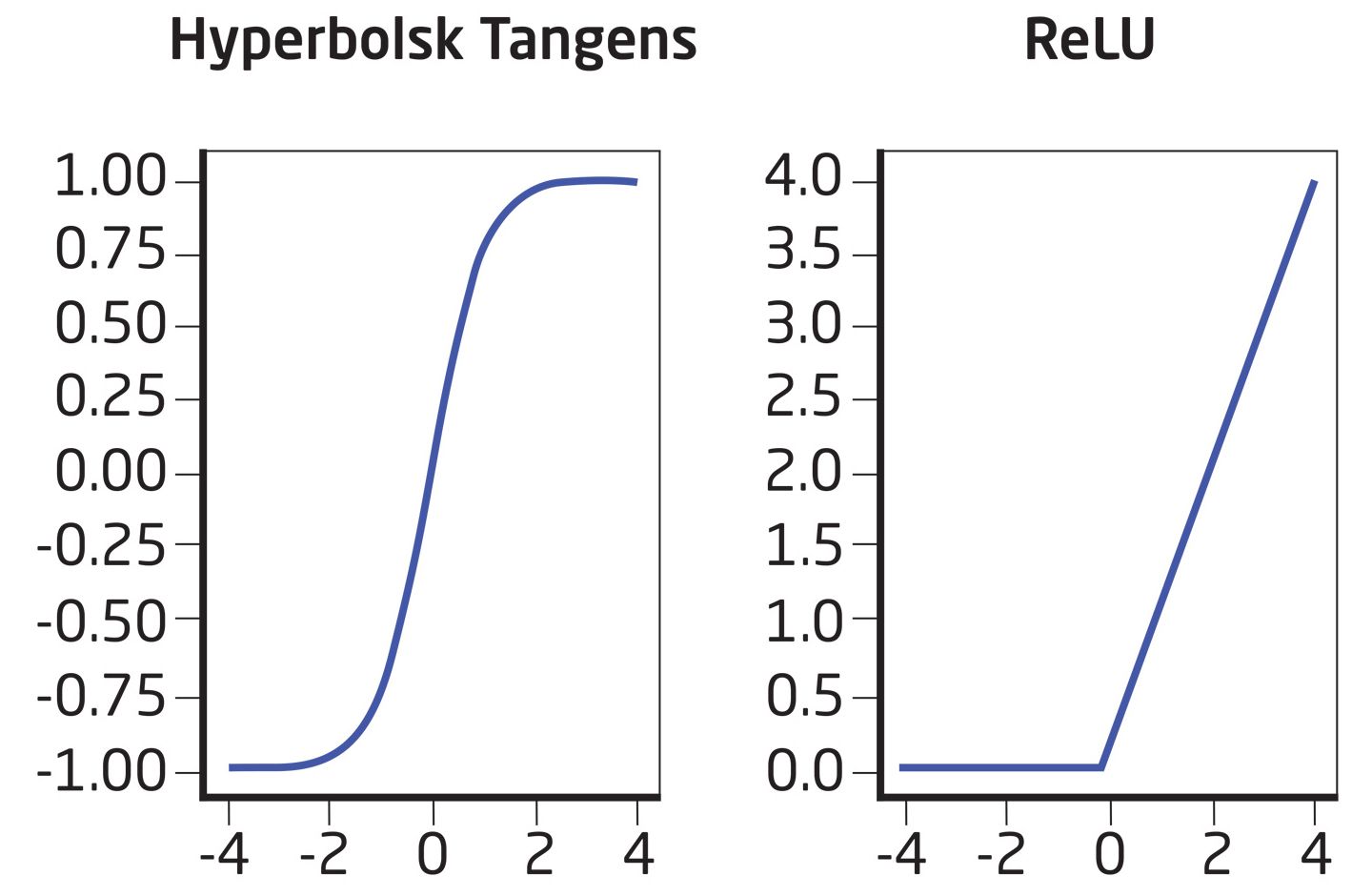
Funktionen hyperbolsk tangens givet ved:

$f (z) = (e^{z} - e^{- z}) / (e^{z} + e^{- z})$

Og ReLU-funktionen (Rectified Linear Unit ) givet ved

$g (z) = {\begin{matrix} z & z \geq 0 \\ 0 & z < 0 \end{matrix}$

Lige som på figuren herover, er $z$ outputtet fra vores lineære neuron. Lad os tage et nærmere kig på sigmoidfunktionen $σ (z)$ .

Opgave 3

A) Plot sigmoidfunktionen $σ (z)$ på din laptop. Hvordan vil du karakterisere den? Hvad er den højeste værdi, funktionen kan antage? Hvad er den laveste?

Vi vil gerne benytte vores sigmoidfunktion, efter at vi har brugt vores lineære neuron på vores data, $x$ . Vi vil altså gerne have at $z$ er output fra et lineært neuron. Prøv at erstatte $z$ med de følgende lineære funktioner og plot sigmoidfunktionen som funktion af $x$ . Hvordan ændre funktionen sig?

$\begin{array}{rcl} z & = & x - 2 \\ z & = & 3 x - 2 \\ z & = & - x + 2 \end{array}$

B) Vis at der gælder at $σ (z) = e^{z} / (e^{z} + 1)$

C) Bestem den afledede $σ^{'} (z)$ af sigmoidfunktionen. Gem resultatet, vi skal bruge det senere. Du kan med fordel skrive dit udtryk ved hjælp af sigmoidfunktioner, dette vil måske gøre resultatet mere overskueligt for dig.

De to andre aktiveringsfunktioner - hyperbolsk tangens og ReLU - er afbildet i figuren her.

Sigmoidfunktionen og konfidens

Forestil dig, at du har to venner, Adam og Karl, der giver dig investeringstips på aktiemarkedet. En dag kommer de begge til dig med to forskellige, rigtig gode tips til investeringer, begge med et stort afkast. Adam siger: Jeg er nogenlunde sikker på, at dette er en god investering. Karl siger: Jeg er 100% sikker på, at dette er en god investering.

Hvilken investering sætter du dine penge på? Nummer to selvfølgelig! Karl er meget mere sikker i sin forudsigelse end Adam. Vi ønsker præcis det samme af vores neurale netværk. Hver gang det neurale netværk laver en forudsigelse, ønsker vi at vide, hvor sikkert netværket er på forudsigelsen, sådan at vi ved hvor meget vægt, vi skal lægge på den.

Vi kalder denne sikkerhed for konfidens når vi beskæftiger os med modeller. En forudsigelse med høj konfidens er altså en forudsigelse, som vores model er meget sikker på, er korrekt. Omvendt er en forudsigelse med lav konfidens en forudsigelse som vores netværk er usikker på.

Men hvordan hænger sigmoidfunktionen og konfidens sammen?

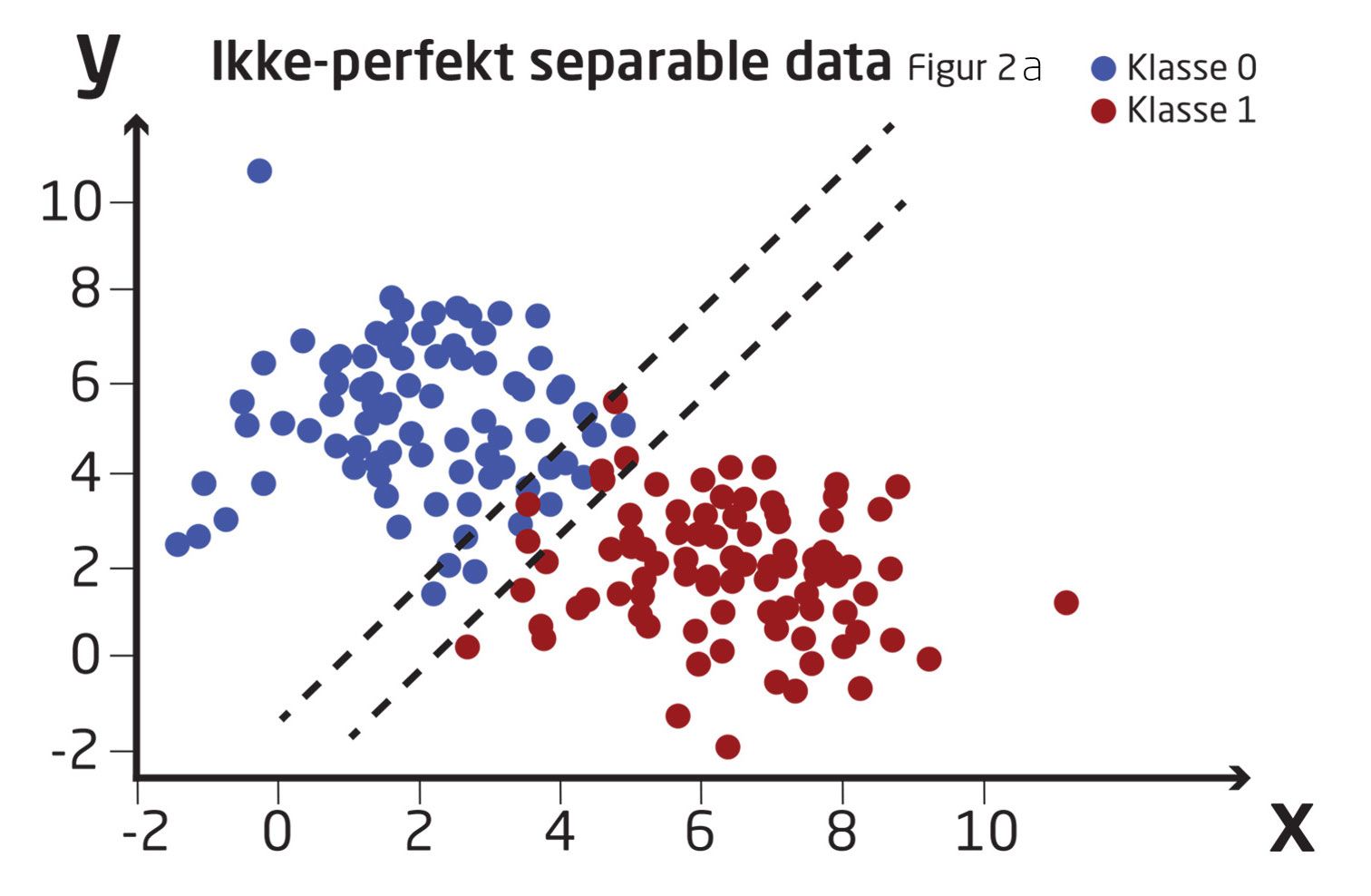
Lad os tage et nærmere kig på vores ikke separable data (Figur 2a).

Vi ser, at vi har to store områder: ét over de sorte linjer, hvor alle datapunkterne klart er i klasse 0, og et andet under de sorte linjer, hvor alle datapunkter klart er i klasse 1. Derudover har vi et lille område imellem de sorte linjer, hvor der er lidt af begge datapunkter. Altså et område, hvor vi vil have lav konfidens i vores forudsigelser.

Vi har altså et stort område (over de sorte linjer) hvor vi er sikre på at datapunkterne tilhører klasse 0, et lille område (mellem de sorte linjer) hvor datapunkterne skifter fra klasse 0 til klasse 1, og et stort område igen (under de sorte linjer) hvor datapunkterne tilhører klasse 1.

Kig igen på vores sigmoidfunktion $σ (z)$ . Den er udformet på denne måde: Mange inputværdier giver et output, der er meget tæt på 0, mange inputværdier giver et output, der er meget tæt på 1, og så et lille interval omkring $z = 0$ , hvor sigmoidfunktionen skifter sin output fra 0 til 1.

Af netop denne grund vil vi bruge sigmoidfunktionen til beregne vores konfidens, når vi beskæftiger os med klassifikation mellem to klasser. Jo tættere $z$ er på 0, jo mere usikker er vores forudsigelse af om data tilhører den ene eller den anden klasse.

Vi kan altså nu udregne vores models konfidens for hver forudsigelse, den laver. Vi mangler dog stadig den nok mest relevante ting, nemlig at finde nogle modelparametre, $w_{x}$ og $b$ , sådan at vores models forudsigelser er korrekte. Så lad os se på, hvordan vi løser dette problem.

Inden vi går videre med med modelparametre, er der dog nogle begreber fra verden af neurale netværk og fler-dimensionelle data, som vi er nødt til at beskæftige os med først.

Terminologi og begreber i neurale netværk

Det er sjældent, at vores datapunkter, $x$ , er en-dimensionelle. Ofte er vores datapunkter fler-dimensionelle. Og det vil derfor være nyttigt at bruge vektorer i forbindelse med vores model.

Vi vil fremadrettet angive et datapunkt som en vektor $\vec{x}$ . Denne vektor består af vores opsamlede data, som vi ønsker at bruge til at bestemme vores klasse med. Har vi f.eks. opsamlet højde, alder og skostørrelse hos en række personer, vil vores data, $x$ , være tre-dimensionelt. Vi vil i dette tilfælde skrive: $\vec{x} = [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}]$ hvor $x_{1}$ er højden, $x_{2}$ er alderen og $x_{3}$ er skostørrelsen.

Vi vil kalde hver af disse tre tal for en feature, og sige at $\vec{x}$ består af tre features. Vores inputdata er ikke begrænset til at være tre-dimensionelt, eftersom vi kan lave lige så mange målinger, vi vil, som udgangspunkt for vores forudsigelse.

Vi vil fremadrettet angive, $\hat{y}$ som det output, også kaldet den forudsigelse, vores model giver. Dette er altså det tal, der kommer ud af vores funktion (model), når vi lægger vores data ind $\vec{x}$ . Vi skriver $\hat{y} = f (\vec{x})$ .

Tilsvarende vil vi angive $y$ som værdien, et datapunkt rent faktisk har. Vi har altså, at hvis $\hat{y} = y$ , så har modellen klassificeret rigtigt! Mens hvis $\hat{y} \neq y$ så har modellen klassificeret forkert!

For at opsummere:

$\vec{x} = [\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{m} \end{matrix}]$ er vores input data. Vi siger at $\vec{x}$ består af de $m$ features, $x_{1}, \dots, x_{m}$
$\hat{y}$ er vores modelforudsigelse.
$y$ er den korrekte værdi.

Hvis vores input data, $\vec{x}$ er $m$ -dimensionelt, så vil vores modelparameter også være det, og vi skriver

$\vec{w} = [\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{m} \end{matrix}]$ .

$\vec{w} \cdot \vec{x}$ vil så være prikproduktet mellem de to vektorer givet som $\sum_{i = 1}^{m} w_{i} \cdot x_{i}$ .

Med disse begreber på plads kan vi nu anvende vores lineære neuron på data af vilkårlig dimension, og vi kan gå i gang med at finde vores modelparametre som lovet i sidste afsnit.

Bestemmelse af modelparametre

Vi starter med at definere en tabsfunktion (loss function) for vores model; denne funktion vil vi kalde $L$ . Tabsfunktionen $L$ , skal måle, hvor god vores model er til at lave forudsigelser. Vi lader os inspirere af regression og definerer vores tabsfunktion, som den kvadrerede fejl.

$L (y, \hat{y}) = (y - \hat{y})^{2}$

Eftersom $\hat{y}$ er en funktion af vores inputdata $x$ , som vi for nemheds skyld vil antage er en-dimensionelt, kan vi også skrive

$L (y, x) = (y - \hat{y})^{2} = (y - σ (w_{x} \cdot x + b))^{2}$

Vi kan nu bruge differentialregning til at bestemme vores modelparametre, $w_{x}$ og $b$ , sådan at vores tab $L$ bliver minimeret.

Opgave 4

A) Differentier den samlede tabsfunktion med hensyn til vores modelparametre. Altså bestem $\frac{\partial L}{\partial w_{x}}$ og $\frac{\partial L}{\partial b}$ ved at benytte kædereglen:

$\frac{d}{d x} h (g (f (x))) = h^{'} (g (f (x))) \cdot g^{'} (f (x)) \cdot f^{'} (x)$

Vink: du kan få brug for dit resultat fra Opgave 3C.

Lad os prøve at indsætte nogle tal i vores udtryk. Antag at vi har et datapunkt, $(x, y) = (- 4, 1)$ og at $w_{x} = 1$ og at $b = 0$ . Ved indsættelse fås at $\hat{y} = σ (w_{x} \cdot x + b) \approx 0.018$ og $L = (y - \hat{y})^{2} = (1 - 0.018)^{2} \approx 0.96$ . Vores tabsfunktion har altså en værdi på 0.96. Kunne man vælge $w_{x}$ og $b$ så $L$ bliver mindre?

B) Indsæt overstående værdier i de udtryk, du har fundet for $\frac{\partial L}{\partial w_{x}}$ og $\frac{\partial L}{\partial b}$ .

Hvis du har løst Opgave 4 korrekt, skal du gerne få at $\frac{\partial L}{\partial w_{x}} \approx 0.136$ og $\frac{\partial L}{\partial b} \approx - 0.034$ .

Disse to tal kan vi nu bruge til at opdatere værdierne for vores modelparametre $w_{x}$ og $b$ , således at værdien af tabsfunktionen $L$ bliver mindre.

Til at gøre dette vil vi bruge Euler's approximation til en funktion $f (x)$ omkring $x = x_{0}$ , altså at:

$f (x_{0} + Δ x) \approx f (x_{0}) + f^{'} (x_{0}) \cdot Δ x$ .

Her er nøjagtigheden af vores approksimation afhængig af, hvor lille $Δ x$ er. Som du kan se på figuren her, hvor funktionen $f (x) = x^{3} + 4 x^{2} - 4 x$ samt dens tangent i $x = 0$ er afbildet, så bliver approksimationen dårlig, hvis $Δ x$ bliver stor. Til gengæld er den lineære approksimation nogenlunde præcis, hvis vi blot sørger for, at $Δ x$ er lille.

Vi vil bruge Eulers approximation til at ændre vores modelparametre $w_{x}$ , sådan at vores tabsfunktion $L$ bliver mindre.

I Opgave 4.B fik du forhåbentlig som resultat, at $\frac{\partial L}{\partial w_{x}} \approx 0.136$ . Dette betyder, at hvis vi øger $w_{x}$ med $Δ w_{x}$ , så vokser $L$ med ca. $Δ w_{x} \cdot 0.136$ . Omvendt forventer vi, at hvis $w_{x}$ mindskes med $Δ w_{x}$ , så vil $L$ aftage med ca. $Δ w_{x} \cdot 0.136$

C) Vælg en værdi for $Δ w_{x}$ . Udregn hvad du forventer, at din tabfunktion formindskes med, når du trækker $Δ w_{x}$ fra $w_{x}$ . Udregn nu $L (y, x) = (y - \hat{y})^{2} = (y - σ ((w_{x} - Δ w_{x}) \cdot x + b))^{2}$ . Sammenlign dit forventede tab med dit aktuelle tab. Hvordan stemmer de overens?

Vi kan nu gøre dette igen og igen, indtil vores tabsfunktion $L$ bliver tilstrækkelig lille. Det er ikke svært at se, at $w_{x}$ og $b$ bliver mere og mere negative, efterhånden som vi gentager denne proces. Til gengæld er det ikke nemt at gætte hvad der ville ske, hvis vi havde mange datapunkter, eller hvis vores model bestod af mere end én neuron.

Som nævnt skal vi under normale omstændigheder (flere neuroner og flere datapunkter), sikre os at $Δ w_{x}$ og $Δ b$ ikke bliver for store. Normalt vælger vi $Δ w_{x}$ og $Δ b$ i størrelsesorden 0.1 til 0.001.

Vi har nu introduceret de byggeklodser, vi skal bruge for at opbygge vores neurale netværk, nemlig neuroner og aktiveringsfunktioner. Derudover har vi fundet en måde at udregne vores models konfidens, sådan at vi ved, hvor sikker vores model er på dens forudsigelser samt iterere os frem til gode modelparametre.

Lad os nu introducere de sidste ting, vi skal bruge for at sikre os, at vores model fungerer optimalt.

I dette afsnit skal vi introducere tilpasning af features eller feature engineering, som det ofte kaldes blandt udviklere af kunstig intelligens. Feature engineering er en måde at skabe nye features ud fra de features, vi allerede har. Hvis vi f.eks. beslutter, at alle $x 1$ -værdier skal kvadreres har vi skabt en ny feature, som stadig siger noget unikt om vores datapunkt, og som muligvis gør det nemmere at separere vores data.

Derudover skal vi beskæftige os med hyperparametre. Hyperparametre er f.eks. antallet af neuroner i vores netværk og er karakteriseret ved, at vi ret frit kan vælge til eller fra, når vi bygger vores neurale netværk.

Feature engineering og valg af hyperparametre gør tit forskellen, om vores netværk virker eller ej. I dette afsnit kigger vi lidt nærmere på begge dele, og du får du lov at prøve selv. Vi skal nemlig i gang med at eksperimentere med vore helt eget neurale netværk. Det gælder for de fleste typer af kodning i dag, at der findes GUIs (Graphical User Interfaces), der gør det muligt at bygge og ændre i dele af koden, uden at vi selv behøver at skrive koden fra bunden.

Vi skal i dette afsnit bruge vores matematiske forståelse af, hvad der foregår i neurale netværk sammen med et sådant GUI for at ændre på vores eget neurale netværk, så det bliver bedre til at gøre, hvad vi beder det om.

Feature Enginering

I afsnit 2 introducerede vi begrebet features som de målinger vores data, $x$ , består af.

Der findes to måder, vi kan lave nye features på:

Den første er at beslutte sig for hvilke målinger vores data skal bestå af. Når du f.eks. måler den gennemsnitlige temperatur, saltindholdet og størrelsen af en sø for at forudsige, hvilke fisk, der er i den. Så har du lavet de tre features saltindhold, gennemsnitstemperatur og størrelse. Denne måde at konstruere features på, kan lade sig gøre, når vi selv indsamler data. Men det er selvfølgelig ikke altid tilfældet.

En anden måde at konstruere disse features på, er at ved at tage en funktion af vores allerede indsamlede features. Hvis vores data f.eks. består af to features, $\vec{x} = [\begin{matrix} x_{1} \\ x_{2} \end{matrix}]$ , så kan vi konstruere en ny feature ved også at bruge $x_{1}^{2}$ som data. Vi har så at
$\vec{x} = [\begin{matrix} x_{1} \\ x_{2} \\ x_{1}^{2} \end{matrix}]$ .

Der er ingen begrænsning på, hvilke funktioner vi kan tage på vores originale features for at skabe nye.

Vi skal senere i dette afsnit se et eksempel, hvor netop det at lave nye features ud fra dem, vi allerede har, gør forskellen om vores model virker eller ej.

Opgave 5

A) Betragt igen datasættet i figur 3. Kan du fremstille en ny feature, der gør, at vi kan separere data i to klasser?

Hjælp: Overvej hvordan du kan bruge koordinaternes fortegn til at lave den nye feature. Er der en anden måde at beskrive hhv. de blå og de røde prikkers placering i koordinatsystemet end ved brug af $(x_{1}, x_{2})$ ?

Hyperparametre

I afsnit 2 beskæftigede vi os med en model, der bestod af et enkelt neuron med en aktiveringsfunktion. Det er yderst sjældent, at et enkelt neuron fungerer som en god model. Derfor har vi tit mere end én neuron - nogle gange op til flere millioner - med i vores model. Dette er grunden til, at vi kalder denne modeltype for neurale netværk. Når vi ønsker flere neuroner i et neuralt netværk kan dette ske på en af følgende to måder: Enten sætter vi neuronerne i parallel, eller også sætter vi dem i serie. I figurerne her kan du se et eksempel, hvor neuroner er sat i parallel (øverst) og et hvor de er sat i serie (nederst).

Matematisk kan vi beskrive to neuroner i parallel som $σ ((w_{1} x + b_{1}) + (w_{2} x + b_{2}))$ . To neuroner i serie kan vi matematisk beskrive som $σ (w_{2} (w_{1} x + b_{1}) + b_{2})$ . Hvor $w_{1}$ og $b_{1}$ og henholdsvis $w_{2}$ og $b_{1}$ er modelparametre for neuron $1$ og neuron $2$ .

Her er $σ$ vores aktiveringsfunktion. Ofte benytter vi én slags aktiveringsfunktion mellem to lag af neuroner, og en anden slags aktiveringsfunktion efter det sidste lag af neuroner. I vores eksempel, hvor vi kiggede på klassifikation med to klasser, var aktiveringsfunktion efter det sidste lag en sigmoidfunktion. Vi vil dog ofte bruge ReLU aktiveringsfunktionen mellem lagene af neuroner.

Vi kalder antallet af neuroner i et netværk for en hyperparameter. Hver gang vi omtaler noget som en hyperparameter, er det fordi det er en parameter, vi skal vælge i vores netværk - i modsætning til vores modelparametre, som vi kunne regne os frem til. Ud over antallet af neuroner kan vi også kalde valget af aktiveringsfunktioner for en hyperparameter: Det er nemlig også frit for os at vælge den aktiveringsfunktion, vi ønsker.

I sidste afsnit, hvor vi skulle vælge en værdi for $Δ w_{x}$ og $Δ b$ , var disse også hyperparametre. Man omtaler i øvrigt ofte denne hyperparameter som læringsraten (på engelsk: learning rate), da den styrer, hvor hurtigt vores modelparametre kan ændre sig, altså hvor hurtigt vores netværk kan lære.

Lad os undersøge effekten af disse hyperparametre nærmere.

Opgave 6

Du skal nu selv prøve at arbejde med hyperparametre og være feature engineer.

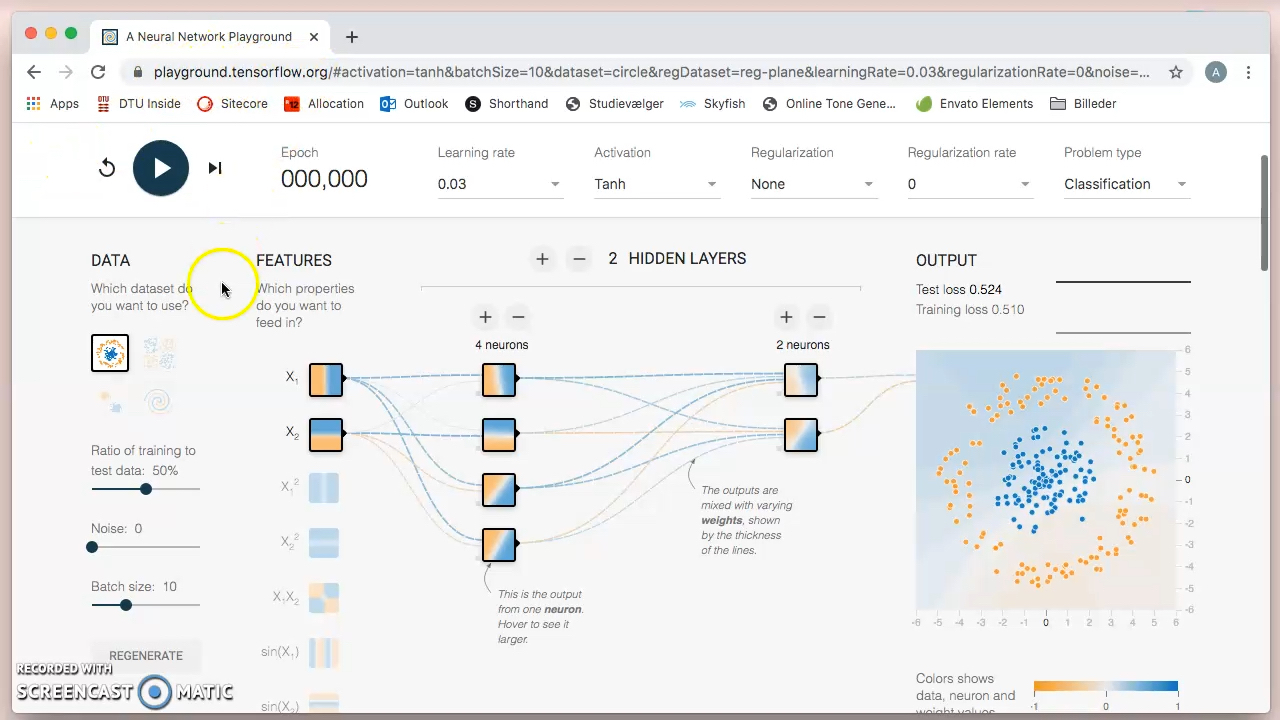
Start med at åbne linket her. Her kan vi lege med små neurale netværk og se nogle af de ting, vi indtil videre kun har snakket om, i aktion:

Neuralt netværk

Øverst på hjemmesiden kan du vælge imellem fem ting. Hvad de betyder, er forklaret herunder.

Learning rate: Dette er vores netværks læringsrate. Det bestemmer, hvor meget vi ændrer vores modelparametre ved hver iteration. Jo lavere tal, jo mindre ændrer vi vores modelparametre ved hver iteration.
Activation: Dette er vores aktiveringsfunktioner. Der er de tre funktioner introduceret herover - tanh, sigmoid og ReLU. Derudover er der linear hvilket svarer til "ingen aktiveringsfunktion".
Regularization: Vil blive forklaret senere i afsnittet.
Regularization rate: Vil blive forklaret senere i afsnittet.
Problem type: Dette bestemmer, om vi ønsker et klassificeringsproblem eller et regressionsproblem (i dette materiale arbejder vi med klassificeringsproblemer, så den indstilling giver sig selv).

Yderst til venstre kan du vælge imellem fire datasæt (de er afbildet). Her er den ene klasse blå og den anden orange.

Under "features" kan du vælge, hvilke features du vil give modellen. Hvert datapunkt består af en $x$ - og en $y$ -koordinat, hhv. kaldet $x_{1}$ og $x_{2}$ . Du kan vælge at sætte disse værdier i anden, gange dem med hinanden eller tage sinus af dem. Du kan vælge hvilke features, der skal inkluderes, ved at klikke på billederne af dem.

Derudover kan du med + og - vælge hidden layers, dette er antallet af lag med neuroner i sekvens. Og neurons, hvilket er antallet af neuroner i parallel i det givne lag.

Du træner modellen ved at trykke på play-knappen. Du kan på figuren under output følge med i, hvordan modellen klarer sig. Her er der også angivet en værdi for 'training loss', dette er værdien af vores tabsfunktion, $L$ .

Vi kan altså ved at ændre på disse ting, se de hyperparametre, vi har introduceret i aktion.

A) Lad os starte med at se et eksempel, hvor vi skal ændre vores originale features for at få modellen til at virke. Gør følgende:

Vælg datasættet øverst til venstre (cirklen med en ring uden om, hvis det ikke allerede er valgt - det er det som regel).
Vælg en learning rate der er mindre end 1. (Den skal være mindre end 1, ellers virker den ikke - forklaringen på dét ligger og gemmer sig i opgave 4, hvis man er meget opmærksom.)
Vælg ReLU aktivering
Vælg none i Regularization
Vælg 0 i Regularization rate
Vælg klassifikationsproblem.
Vælg antal "hidden layers". Du kan frit vælge hvor mange lag der skal være.
Vælg hvor mange neuroner der skal være i hvert lag. Du kan frit vælge antal.
Eksperimentér med at fra- og tilvælge de forskellige features, indtil det neurale netværk er i stand til at klassificere tilfredsstillende. Hvor få features kan du nøjes med? Hvilke features virkede? Hvordan kan det være? Kan du finde nogle features, der virker uanset netværkets størrelse?

Hjælp: Overvej om cirkelens ligning kan bruges til at bestemme hvilke features som fungerer bedst.

Du kan her se, hvordan man gør:

Jo simplere des bedre: Jo mindre netværk, du er nødt til at bygge op omkring dine features for at de virker, jo stærkere er de i sig selv - og vi ønsker at bruge de bedste byggeklodser i vores netværk. Simplere netværk er desuden hurtigere og kræver mindre tid, computerkraft, strøm etc.

B) Vælg dit eget datasæt blandt de tre andre. Eksperimentér med hyperparametrene og se, hvordan det påvirker modellen. Sammenlign med en anden fra klassen, der har valgt det samme datasæt. Hvor forskellige er jeres hyperparametre? Hvilken af jeres modeller virker bedst?

Hjælp: Du kan ændre learning rate, mens modellen træner. Hvis dit outputbillede eller dit training loss hopper meget, så er learning rate formentlig for høj.

Det er ofte helt afgørende for, om vores model virker eller ej, at vi vælger de rigtige hyperparametre. Hvis vi f.ex vælger for få neuroner, kan vores model ikke lave gode forudsigelser - vi siger at det ikke har kraft nok. Vælger vi til gengæld for mange neuroner, kan vores model blive meget langsom at træne, da der er mange modelparametre, der skal itereres over. Derudover kan et for stort netværk lide af et begreb kaldet overfitting. Lad os se nærmere på overfitting og hvordan vi kan undgå det.

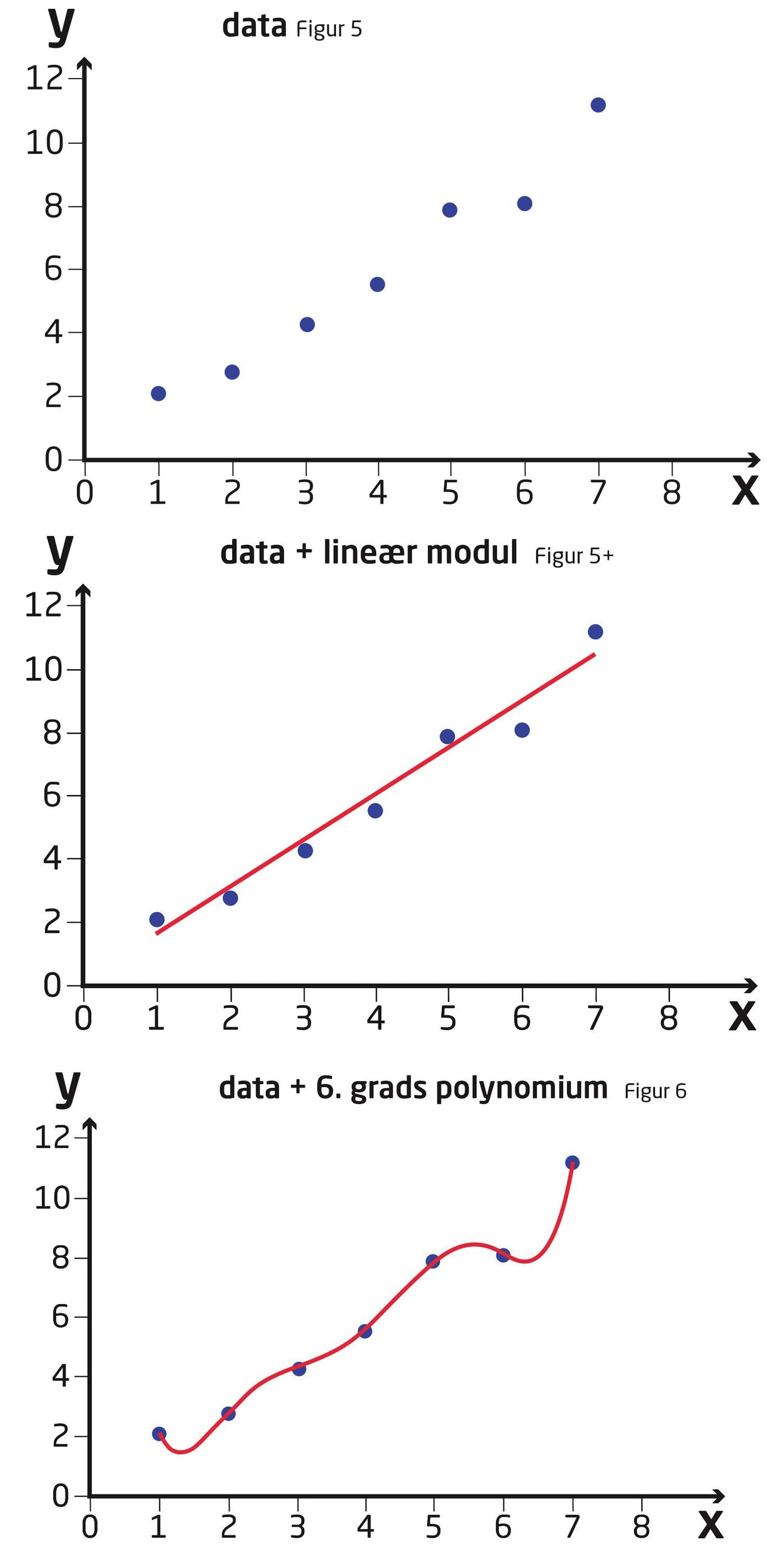
Forestil dig, at vi er givet følgende data (Figur 5):

Vi ønsker nu, ud fra disse data, at finde en model, vi kan bruge til at forudsige nye datapunkter med. Et godt bud være, at bruge en lineær funktion: $f_{1} (x) = a x + b$

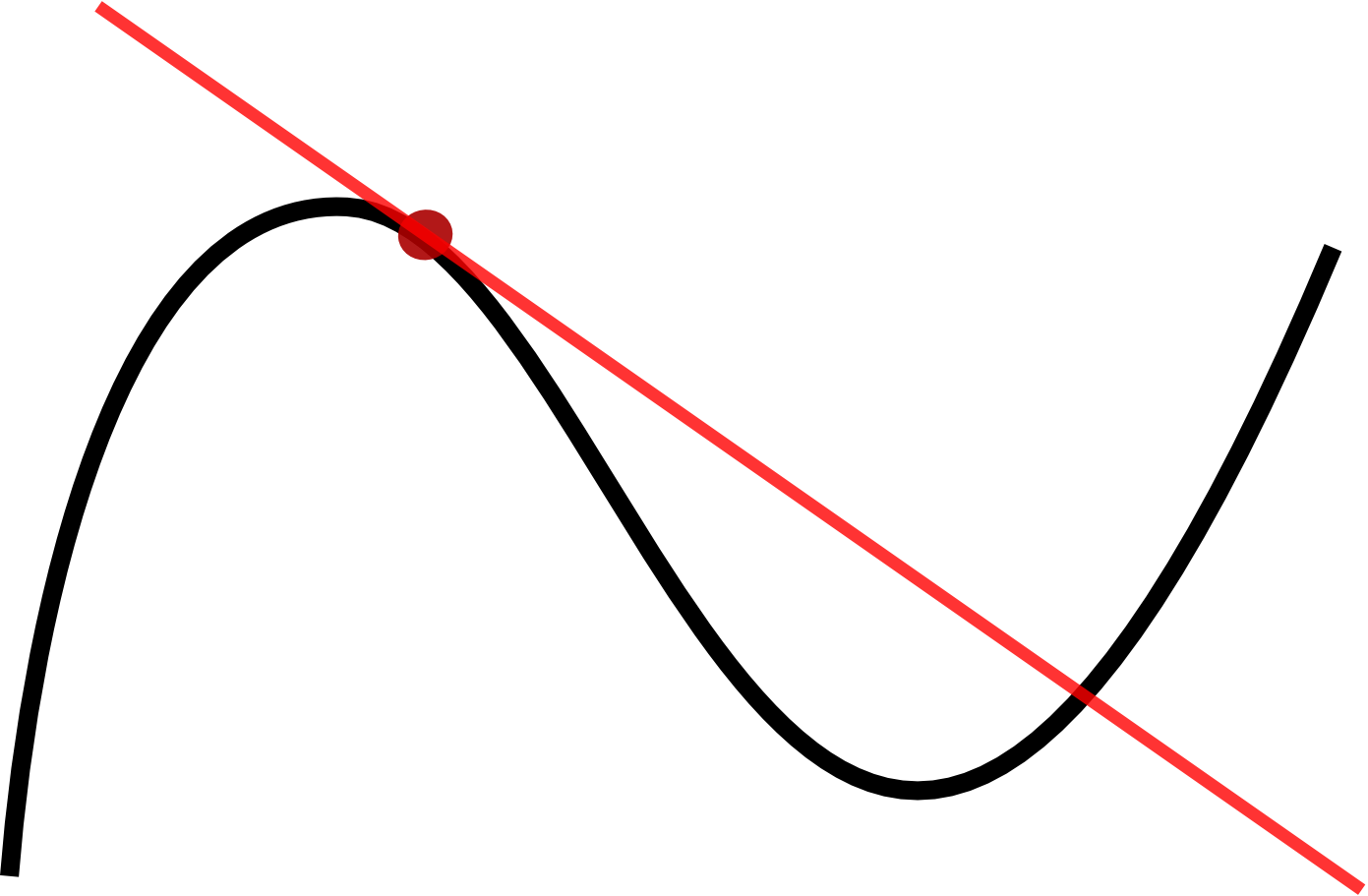
Hvis vi bestemmer den bedst mulige lineære funktion, får vi i dette tilfælde: $\hat{y} = 1.48 x + 0.08$ . Den lineære funktion er afbildet på Figur 5+ sammen med vores datapunkter. Vi kan umiddelbart se, at den virker som en udemærket model. Modellen har følgende gennemsnitsfejl: $\frac{1}{6} \sum_{n = 1}^{6} ({\hat{y}}_{n} - y_{n})^{2} = 0.27$ . Gennemsnitsfejlen er altså ikke nul, men tæt på.

Lad os nu se hvad der sker, hvis vi i stedet vælger polynomium med højere orden som vores model, f.ex. et 6. grads polynomium $f_{6} (x)$ . I dette tilfælde fås at den bedste model er:

$\begin{array}{rcl} \hat{y} & = & 0.03 x^{6} - 0.61 x^{5} + 5.54 x^{4} - 25.3 x^{3} \\ + & 60.48 x^{2} - 69.72 x + 31.73 \end{array}$

I Figur 6 er $f_{6} (x)$ afbildet sammen med vores datapunkter. Vi ser at polynomiumet rammer alle vores datapunkter, og har altså gennemsnitsfejl, $\frac{1}{6} \sum_{n = 1}^{6} ({\hat{y}}_{n} - y_{n})^{2} = 0$ . Selvom $f_{6} (x)$ går igennem alle vores datapunkter, virker denne model dårligere end vores lineære model $f_{1} (x)$ . For selv om den rammer alle kendte punkter, virker det ikke realistisk, at den vil ramme ukendte punkter i systemet ret præcist.

Som eksempel antager vi, at vi gerne vil forudsige $y$ når $x = 8$ . Vi har målt dette datapunkt på samme måde som de andre, og har fundet at datapunktet er givet som $(8, 11.7)$ . Hvad siger vores modeller her?

Funktionen $f_{1} (x)$ forudsiger, at ${\hat{y}}_{8} = f_{1} (8) = 11.9$ , hvilket giver fejlen $(11.9 - 11.7)^{2} = 0.04$ . Igen ser vi en lille fejl.

Tilsvarende forudsiger $f_{6} (x)$ at ${\hat{y}}_{8} = f_{6} (8) = 61.3$ , hvilket giver en fejl på $(61.3 - 11.7)^{2} = 2459$ . Vores 6. grads polynomium $f_{6} (x)$ er altså helt galt på den, når vi ønsker at lave forudsigelser.

Vi siger, at vores 6. grads polynomiums model har overfittet, dvs. at modellen klarer sig godt på det data, vi har brugt til at finde modellens parametre med, men klarer sig dårligt, når den skal lave nye forudsigelser. Man ser ofte dette ske, når en model har for mange modelparametre i forhold til hvor mange datapunkter der er tilrådighed.

Vi ser altså, at en lav gennemsnitsfejl på vores givne data ikke nødvendigvis giver en god model. Vi må altså stille os selv to spørgsmål:

Hvordan måler man hvor god en model er?
Hvordan undgår man at en model overfitter?

Vi har allerede set en metode til at evaluere vores model, som giver et mere retvisende billede. I eksemplet før, hvor vi havde et ekstra datapunkt, $(8, 11.7)$ , kunne vi bruge dette til at evaluere vores to modeller i forhold til hinanden.

Træningssæt og evalueringssæt

Som vi kan se ovenfor, er det en god ide at teste sin model på data, som ikke er blevet anvendte til at bestemme vores modellens parametre.

For at evaluere neurale netværk, vil vi derfor dele vores datapunkter op i to dele:

Den ene del bruger vi til at bestemme vores modelparametre med, denne del kaldes et træningssæt.

Den anden bruger vi til at evaluere, eller teste, vores model med, denne del kaldes et testsæt.

Ofte benyttes et 80%/20% split af datamængden til trænings- og testsæt, men det er op til dig selv, hvordan du deler datasættet op. Det er dog vigtigt, at testsættet er stort nok til at evaluere modellen retvisende.

Denne opsplitning giver os et fingerpeg om, hvordan vores neurale netværk reagerer på nye data, hvilket jo er det vi er interesserede i. Og derudover giver det os mulighed for at detektere, om modellen har overfittet ved at se på differencen mellem tab for træningssæt og tab for testsæt.

Opgave 7

A) Ud over at testsættet skal være stort nok til at evaluere modellen retvisende, skal det også være valgt tilfældigt. Diskuter i klassen, hvorfor testsættet skal være valgt tilfældigt.

Dette besvarer vores første spørgsmål om, hvordan vi kan evaluere vores model retvisende. Vi har dog stadig ikke svaret på, hvordan vi undgår overfitting, så lad os se nærmere på det.

Fra testsæt til regulering

I vores eksempel før var det ikke besværligt at se, at et 1. grads polynomium var tilstrækkeligt, når vi kiggede på vores datapunkter. Dette kan dog ikke altid lade sig gøre i praksis, hvor høj-dimensionelle datasæt og manglende muligheder for at visualisere problemet gør det mere komplekst.

Vi har med andre ord brug for en bedre metode end blot at se på vores data til at undgå overfitting.

Lad os starte med at kigge på de to polynomier, vi brugte som modeller tidligere:

$\begin{array}{rcl} f_{1} (x) & = & 1.48 x + 0.08 \\ f_{6} (x) & = & 0.03 x^{6} - 0.61 x^{5} + 5.54 x^{4} - 25.3 x^{3} \\ + 60.48 x^{2} - 69.72 x + 31.73 \end{array}$

Læg mærke til hvordan vores model, der lider af overfitting, har store koefficienter i forhold til datapunkternes værdi og samlede spænd. Dette er ikke tilfældigt. Normalt, når en model lider af overfitting, ser vi at modelparametrene bliver store. Dette er en god nyhed, da vi blot kan begrænse hvor store vores modelparametre kan være. Dette gør vi ved at modificere vores tabsfunktion, $L$ .

Tidligere lod vi vores tabsfunktion være givet som $L = (y - \hat{y})^{2}$ . For at undgå overfitting vil vi addere størrelsen af vores modelparametre til denne tabsfunktion, sådan at den nu er givet ved

$L = (y - \hat{y})^{2} + α | \vec{w} |$ .

Her er $| \vec{w} |$ længden af vektoren $\vec{w}$ , som består vores $m$ vægte i det neurale netværk. Altså er $| \vec{w} |^{2} = \sum_{i = 1}^{m} w_{i}^{2}$ .

Og $α$ er en hyperparameter, der styrer hvor vigtigt det er at vægtene er små, i forhold til hvor vigtigt det er at vi laver få klassifikationsfejl.

Dette betyder, at når det neurale netværk iterere sig frem mod modelparameterne, så er det denne nye tabsfunktion, $L$ , der skal differentieres.

Opgave 8

A) Forklar hvilken effekt det har på vores model, når værdien af $α$ øges eller mindskes.

B) Åben linket her igen. Start med at vælge følgende:

Neuralt netværk

Vælg det øverste datasæt til venstre (de to cirkler).
Vælg igen en learning rate under 1, ReLU aktivering, ingen Regularization og 0 i Regularization rate, samt vælg klassifikationsproblem. Vælg derudover de features, du ønsker.
Vælg igen frit et netværk (layers og antal neuroner i hvert layer) ved at klikke på + og -.
Under Data, sæt Ratio of training to test data til 10%. (Vi har ikke ret meget træningsdata, men til gengæld meget data at teste på).
Under data, sæt Noise til 20. (Vores datapunkter kommer til at overlappe mere, jo højere dette tal er.)
Træn netværket, til det er færdigt. (Du skal muligvis sætte learning raten ned under træning.) Under output kan du se både dit testtab (test loss) og træningstab (training loss). Netværket er færdigt med at træne, når training loss ikke længere formindskes, eller kun ændrer sig meget lidt og meget langsomt. Beskriv hvad du ser: Hvordan ser det blå område på figuren ud? Hvordan er dit test loss i forhold til dit training loss? Er der overfitting?

Du kan se, hvordan man gør i videoen her:

PS. Du har måske også fået øje på funktionen Batch Size - det betyder ikke noget i dette eksempel og du kan bare lade den stå på hvad den enten er sat til default.

C) Gentag ovenstående i et nyt browser vindue, sådan at du kan se begge figurer samtidigt, men vælg nu L2 under Regularization og vælg 0.01 (for store til medium størrelse netværk) eller 0.1 (for medium til små størrelse netværk) som Regularization rate. Beskriv hvad du ser igen: Hvordan ser det blå område på figuren ud. Hvordan er dit test loss i forhold til dit training loss? Er der overfitting?

Se, hvordan man gør her:

Hvis du er i tvivl om, hvilken regularization rate du skal vælge, så prøv begge og behold det bedste resultat.

D) Sammenlign dit resultat fra B) og C) med andre fra klassen. Da jeres data er trukket tilfældigt, har I højst sandsynligt ikke samme resultater.

E) Udregn forholdet mellem Test loss og Training loss, for det netværk, der ikke er reguleret. Sammenlign i klassen netværket med den største værdi, og dét med den mindste. Det med størst værdi lider mest af overfitting, det med lavest værdi lider mindst. Diskuter i klassen, hvorfor det ene netværk lider mindre af overfitting end det andet.

Vi har nu set, hvordan vi kan evaluere vores neurale netværk retvisende, samt hvordan vi undgår at vores neurale netværk overfitter! Det eneste der mangler nu er at prøve det af i praksis!

Vi er nu nået til der, hvor det bliver rigtig sjovt: I skal bygge jeres eget neurale netværk og benytte det på klassificeringsproblem med to klasser. De data som I skal bruge til at træne og teste jeres netværk skal I også selv indsamle.

Dette skal I bruge til øvelsen

Denne øvelsesvejledning
Smartphone
Computer
Adgang til Google Drev

0: FORBEREDELSE OG OPTAGELSE AF LYDE

Læs hele øvelsesvejledningen igennem.

Download app'en Awesome Voice Recorder til jeres smartphones. I kan finde den her:

iPhone

Android

Inden I går i gang med øvelsen skal I sørge for at app'en optager lyde i det rigtige format. Tryk på det lille tandhjul nederst til højre for at komme ind på indstillinger (bemærk, at app'en ser anderledes ud på Android-telefoner)

I skal nu sætte filformat til MP3 og bit rate til 320kbps eller 256kbps som vist herunder. I er nu klar til at optage lyde:

I skal opsamle lyde og inddele det i to klasser. Her er der flere forskellige muligheder:

I kan f.eks. vælge at samle lyd ind fra fugle som den ene klasse og biler som den anden.
I kan også vælge mere avancerede og fintmaskede opdelinger, f.eks. kan I opdele kategorien biler på små veje eller på store veje.
Eller I kan blande flere ting sammen i den ene klasse, sådan at den består af fugle, søer og husdyr, mens den anden består af menneskemængder, kirkeklokker og toge. Der er frit valg til hvilke lyde, du synes skal være hvor!

I skal nu ud og indsamle jeres data. I skal lave en række lydoptagelser til de to klasser I har valgt. Optagelserne skal vare 30 sekunder. Når I har optaget en lyd kan I gemme den ved at trykke her:

Giv lydene et passende navn og tryk gem (på Android kan I først navngive filerne efter de er blevet gemt). Når I er færdige med at optage lyde skal I dele optagelserne med jer selv og downloade dem på jeres computer. For at finde lydene i app'en skal I trykke på det lille mappe-ikon nederst til venstre:

Lydene ligger under mappen Default (på Android ligger de under All). Når I er inde i mappen kan I dele dem ved at trykke på den lille pil:

I skal nu vælge Del. Der er forskellige muligheder for at dele lydene. I kan eksempelvis sende dem til jeres emailadresse og hente dem ned på jeres computer:

I skal nu bruge tre programmer. I det første skal I lave de data som skal til at træne netværket, I det andet skal I lave jeres model og i den sidste skal I teste modellen på jeres egen indsamlede data.

1. PRE-PROCES

Vi skal nu lave vores trænings-data. Helt præcist skal vi have hentet vores trænings-data fra to YouTube videoer som I skal vælge. Dette træningsdata skal vi så have delt op i mindre lyd-bidder, kørt dem igennem et stort neuralt netværk og lavet plots, sådan at I kan se, hvordan jeres data ser ud som spektrogrammer.

Inden I begynder skal I oprette en mappe på jeres Google Drev, som hedder "Regn Lyden Ud Opgave". I denne mappe skal I desuden oprette en undermappe med navnet "Plots". Herefter er I klar til at starte.

Følg linket her. Læs vejledningen igennem grundigt inden I starter.

1. PRE-PROCESS

Når I åbner linket skal I som det første trykke på "Open in playground". Dette giver jer mulighed for at køre programmet. I finder den lige under menulinjen her:

I skal nu indsætte jeres Youtube-videoer. I skal indtaste deres url, give dem et passende navn og indtaste længden på de lyd-bidder programmet skal lave. I skal sætte længden til 30 sekunder, så det svarer til længden på de lydoptagelser I selv optager.

Nu skal I give programmet adgang til Google Drev. Når I giver adgang kan programmet gemme lyd-bidder og spektrogrammer på jeres Drev.

Nu kan I køre selve programmet ved at trykke play. Programmet inddeler jeres valgte videoer i mindre lyd-bidder og laver samtidig spektrogrammer, som I kan finde inde på jeres drev, når programmet er kørt færdigt. Det kan sagtens tage mere end 5 minutter før programmet er færdigt, så I skal have tålmodighed. I kan her se en gennemgang af, hvordan I skal gøre her:

Når programmet er færdigt får I følgende besked:

I kan nu finde lyd-bidder og spektrogrammer på jeres drev som vist her:

Nu er I klar til at lave jeres model.

2: LAV JERES MODEL

Nu skal vi bygge jeres model. I skal selv vælge modellens hyper-parametre (learning rate, regulering, antal lag, antal neuroner, aktiverings-funktioner samt antallet af epoker vi skal træne modellen) Følg linket her og læs det igennem grundigt inden I starter:

2. DIN MODEL

I trykker igen "Open in playground". Nu skal I vælge jeres hyperparametre og indtaste dem i programmet. Når I har indtastet dem kan I trykke play.

I skal igen give adgang til Google Drev på samme måde som tidligere. Når I har gjort det kan I starte programmet og træne jeres model med de valgte parametre. I kan her se en gennemgang:

Nu skal I teste jeres model.

3. TEST JERES MODEL

I skal nu teste jeres model på jeres egen indsamlede data.

I jeres "Regn Lyden Ud Opgave"-mappe på jeres Google Drev skulle I gerne kunne finde en mappe ved navn "Test_Data" med 2 undermapper - en til hver kategori. Hvis ikke skal I køre de første to programmer igen. Når I har delt og downloadet jeres egne lydfiler kan I uploade dem i de to mapper:

Når I har uploadet jeres data kan I starte det sidste program. Husk at trykke på "Open in playground", når I starter.

3. TEST DIN MODEL

I skal igen give programmet adgang til Google Drev. Når I har gjort det kan I køre programmet, som tester modellen på jeres lydfiler. Hvis modellen virker perfekt får I følgende resultat for begge kategorier:

Hvis modellen har kategoriseret alle lydene korrekt vil I få en accuracy på 1. Hvis det ikke lykkes, kan I prøve at gå tilbage og forsøge at ændre på jeres valgte hyper-parametre.

I kan her se en gennemgang af, hvordan I tester jeres model:

Nu har I ved hjælp af lyd-bidder fra youtube-videoerne lavet en model, som kan forudsige om en lyd hører til den ene eller den anden kategori. I kan finde spektrogrammer af jeres indsamlede lyde på jeres Google Drev, når I har kørt programmet færdigt i mappen "Plots" under "Test_Data".

Regn Lyden Ud – i matematiktimen er udviklet på DTU. Materialet tager afsæt i et forskningsprojekt ved Center for Makroøkologi, Københavns Universitet, der havde til formål at kortlægge lyden af Danmark. Forskningsprojektet brugte kunstig intelligens til at analysere de indsamlede lyde – og den del af projektet var DTU ansvarlig for. Regn Lyden Ud – i matematiktimen giver et fagligt indblik i, hvordan den kunstige intelligens kan bruges til formålet.

Regn Lyden Ud - i matematiktimen er forfattet af Jacob Johansen (ingeniør uddannet på DTU med speciale indenfor kunstig intelligens), Jesper Spangsmark Nielsen (chefkonsulent, DTU) og Simon Pedersen (gymnasielærer i matematik og fysik). Materialet er redigeret af Andreas Ussingø (DTU) og Christina Madvig Christensen (DTU). Tak til Rasmus Høegh (DTU) for inspiration.

Undervisningsmaterialet er økonomisk støttet af Uddannelses- og Forskningsministeriet / Forskningens Døgn.

Regn Lyden Ud - i Matematiktimen

1 Klassifikation

Klassifikation - et centralt element i læring

Regression

Opgave 1

Opgave 2

2 Aktiveringsfunktioner og Konfidens

Aktiveringsfunktioner og konfidens

Det lineære neuron

Aktiveringsfunktioner

Opgave 3

Sigmoidfunktionen og konfidens

Terminologi og begreber i neurale netværk

Bestemmelse af modelparametre

Opgave 4

3 Feature Engineering og hyperparametre

Feature Enginering

Opgave 5

Hyperparametre

Opgave 6

Neuralt netværk

4 OVERFITTING

Træningssæt og evalueringssæt

Opgave 7

Fra testsæt til regulering

Opgave 8

Neuralt netværk

5 Time to engineer

0: FORBEREDELSE OG OPTAGELSE AF LYDE

iPhone

Android

1. PRE-PROCES

1. PRE-PROCESS

2: LAV JERES MODEL

2. DIN MODEL

3. TEST JERES MODEL

3. TEST DIN MODEL

6 Hvem står bag